En intressant frågeställning för mig som novis inom området är, kan jag lita på matematiken? Frågan blev inte mindre intressant efter att funderingarna kring medvetandet i kapitel 3 tagit form. Själv är jag ingen matematiker, utan en pensionerad båtbyggare, så ber om överseende med, om följande framställningen upplevs som svår att följa.
Matematiken med dess regelverk är utformad för att överensstämma med den logik som kännetecknar vårt medvetande. Att hävda att man tillfullo förstår därför att man via matematik lyckats härleda ett resultat behöver därför inte nödvändigtvis vara sant och/eller beskriva helheten. Det är därför viktigt att förstå att matematiken återspeglar den ”atomära” verklighet vi tycker/anser oss förnimma. Det vi ej direkt förnimmer, det ”imaginära, Bortom Standard-
Modellen,BSM, och ”bortom bergen blommorna och sången”, vilket är en viktig del av konceptet, beskrivs ej av matematikens reella regelverk.
De imaginära talen, som symboliserar det vi ej förnimmer, är t.ex. en konsekvens av detta. För mig personligen ter det sig därför absurt och manipulerat att, som vissa gör, näst intill betrakta matematiken som den Gud, via vilken universum och dess uppkomst kan förklaras. Enligt föregående kapitel är därför resultat erhållna via enbart matematik inte likvärdigt med att förstå helheten inkl. överordnade mer abstrakta samband. Det är därför i sammanhanget värdefullt att sätta sig in i, och begrunda, matematikens ursprung för att se och förstå dess begränsning.
Det ursprung vi syftar på här har inget med matematiska härledningar att skaffa, utan måste enligt konceptet härledas till mekanismer i underliggande strukturer, kompletterat med medvetandets mekanismer. För detta krävs det att vi förstår skillnaden mellan atomärt respektive universellt perspektiv, och då måste medvetandets struktur och mekanismer inkluderas i resonemanget. Matematik, i den form vi känner till och tillämpar, är enbart baserat på ett ensidigt atomärt perspektiv. Det som i litteraturen beskrivs som ”rumtid” kan därför ses som en förenkling, som tillgrips när matematiken, p.g.a. sin begränsning inte förmår ge den sanna helhetsbilden av universum.
Matematikens regelverk är utformat för att återspegla den förnimbara verkligheten inkl ”rum-tid”, i överensstämmelse med den logik som kännetecknar vårt medvetande. Det förefaller mot den bakgrunden logiskt att inleda med ansatsen att försöka finna en atomär vxv-modell, som inkluderar och överensstämmer med matematikens regelverk i kombination med de egenskaper som kännetecknar de elektromagnetiska fälten.
Då de elektromagnetiska fälten beskrivs som teoretiska matematiska konstruktioner av komplex natur blev det i mitt fall Eulers formel ez = ex+jy = ex(cos y + j sin y) som fick bli nästa avstamp. I det fall man i Eulers formeln sätter x = π får man ett samband mellan de fem viktigaste talen inom matematiken, e, i , π, 1 och 0, och den i sammanhanget viktiga cirkulära formen som kännetecknar naturkonstanterna. Eulers formel kan därigenom tillämpas för att beskriva och verifiera det för konceptet helt avgörande, och lika viktiga som fundamentala atomära sambandet, mellan exponentialfunktionen och de trigonometriska funktionerna ingående i växelverkan. Den cirkulära formen sammanlänkar i sin tur, via referensberoende skalära relationer/samband, Eulers formel med naturkonstanterna, εο och μο, och därmed finns sannolikt även allt underlag som krävs för att bl.a. beskriva de elektromagnetiska fälten och fenomenet tid. Det är ingen överdrift att påstå att Eulers formel besitter en exceptionell kapacitet och skönhet.
Då negativa tal utgör en viktig ingrediens i följande resonemang bör nämnas att inom matematiken definieras negativa tal som tal som är reella och mindre än noll. Negativa tal kan här även ses oss ett sätt att representera motsatser, vilket bättre passar in på innebörden i följande text.
I ett historiskt perspektiv gjordes en överraskande matematisk upptäckt efter införande av de komplexa talen (z = x+ jy) och funktioner av komplexa tal. Det visade sig att exponentialfunktionen ex och de trigonometriska begreppen cos x och sin x stod i ett tidigare dolt förhållande/samband till varandra, vilket alltså framgår och uttrycks av Eulers formel, uppkallad efter Leonhard Euler. Formeln utgör ett närmast perfekt verktyg för att beskriva principerna DRP, MP, och DYR samt de i konceptet tillämpade SKALÄRA ”tänjningsfenomen” som ligger till grund för ”skalfaktorerna” ingående i växelverkan-modellen.
Några av de för konceptets växelverkan viktigaste matematiska sambanden som bör behärskas för att aktuella principer ska vara lättillgängliga, åskådliggörs av följande.
Förutsatt att j är konstant, erhålls derivatan vid pos exponent (referens A), och atomär projektion, (y = xn dy/dx = +n xn–1), enligt följande.

Förutsatt att j är konstant, erhålls derivatan vid neg exponent (referens B), och atomär projektion, (y = x–n dy/dx = –n x–n–1 = –n x–(n+1)), enligt följande.
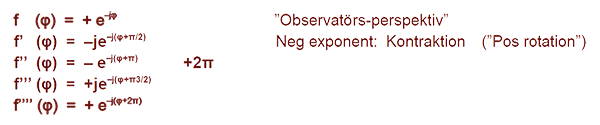
Detta gäller ÖMSESIDIGT, alltså ur båda vxv-perspektiven!
Notera 90-graders DIFFERENSEN, (±j), mellan positiv och negativ exponent!
Differensen medför SKALÄRA effekter!
SKALFAKTORN skiljer expansion och kontraktion från varandra!
Balanskriteriet 2Ư har sin principiella grund i dessa samband.
Genom att skriva, e+jφ/e+jφ = 1 , där 1/ e+jφ = e–jφ , och med kännedom om att,
e+jφ = cos φ + j sin φ +j e+jφ = +j(cos φ + j sin φ) = – sin φ + j cos φ
e–jφ = cos φ – j sin φ –j e–jφ = –j(cos φ – j sin φ) = – sin φ – j cos φ
erbjuder Eulers formel, fortsättningsvis ett hjälpmedel för att normera aktuella samband. Notera här hur derivatan skiftar reella och imaginära termer.
PRODUKT
PRODUKT kan betraktas som en ”mängdkontakt” mellan motriktade referensberoende funktioner. Det kan även uttryckas som ”kontakten” mellan referensberoende interferensbaserade koncentrationsavvikelser. Produkten kännetecknas av vinkeln φ.
e+jφ·e–jφ =(cos φ + j sin φ) · (cos φ – j sin φ) = cos2 φ – j cos φ sin φ + j cos φ sin φ + sin2φ = cos2 φ + sin2 φ
Beloppet av produktmedelvärdet erhålls som, √cos2 φ + sin2 φ = ± 1
Tecknet refererar till ”kommunikationens” RIKTNING. (+ resp -, beroende av aktuell MP/DRP)
KVOT
KVOT kan ses som ”avvikelsefördelning” alt. ”tänjningsfördelning” mellan motriktade funktioner. Täljare och nämnare i kvoten representerar här olika G-koncentrationer, ur olika MP-perspektiv. Perspektiven refererar till skilda MP-förankringar och kan betraktas som olika skalfaktorer. Kvoten kännetecknas av dubbla vinkeln, 2φ. Vinkeln 2φ utgör grund för det ”virtuella” ”imaginära navet”, ± j, och därav följande/beroende begrepp ”INTERNT” resp. ”EXTERNT”.
e–jφ / e+jφ = (cos φ – j sin φ) / (cos φ + j sin φ) = (cos φ – j sin φ) (cos φ – j sin φ) =
= (cos φ – j sin φ)2 = cos2 φ – sin2 φ – j 2 cos φ sin φ = +e–j2φ =
e–j2φ = cos 2φ – j sin 2φ
Kvot-medelvärdesbeloppet erhålls som, √e–j2φ = ±e–jφ (≈ ”verklighets-perspektiv” ≈ objekt)
Ur motsatt MP-förankrat ”maskerat” perspektiv erhålls på likartat sätt,
e+jφ / e–jφ = (cos φ + j sin φ) / (cos φ – j sin φ) = (cos φ + j sin φ) (cos φ + j sin φ) =
= (cos φ + j sin φ)2 = cos2 φ + j cos φ sin φ + j cos φ sin φ – sin2 φ =
= cos2 φ – sin2 φ + j 2 cos φ sin φ = +e+j2φ =
e+j2φ = cos 2φ + j sin 2φ
Kvot-medelvärdebelopp erhålls som, √e+j2φ = ±e+jφ ( ≈ ”MP-förankring” ≈ subjekt)
Ur resp DRP-perspektiv roterar alltså, i kvot-fallet, motsatt perspektiv åt motsatt håll! Den s.k. dubbelrotationen har sin principiella grund i detta.
Växelverkan, VXV, innefattar skilda DRP/MP perspektiv, vars VXV-kvot-medelvärden ges av,
√e+j2φ ·–e–j2φ = √–e0 = ± j (refererar till olika MP-förankringar/”verklighetsperspektiv”!)
VXV-kvot-medelvärdet utgör den basala bakgrunden till de elektromagnetiska fälten. Medelvärdet uppträder vinkelrätt mot ”vxv-kommunikationsriktningen”, ur subjektets perspektiv.
KOMBINERAD PRODUKT & KVOT
KVOT kan här betraktas som en typ av normerad PRODUKT. Konceptet använder sig vid växelverkan, av kombination av PRODUKT och KVOT, via Eulers formel. Produkt och kvot är i grunden komplexa fenomen. Medelvärdet av produkt respektive kvot är Dock enligt ovan reellt respektive imaginärt vid balans mellan aktuella perspektiv. Kombinationen av produkt och kvot BALANSERAR alltså varandra under vissa förutsättningar.
BINOMIAL-TEOREMET
Vid utvärdering av begreppet relativitet i kapitel 16 är det värdefullt att känna till binomial-teoremet,
(x+y)n = yn (1+x/y)n = Ʃ(nk)xk yn-k
Teoremet visar att √(1 + (V/C)2) ≈ 1 / √(1 – (V/C)2) vid små värden på V, och vice versa.

